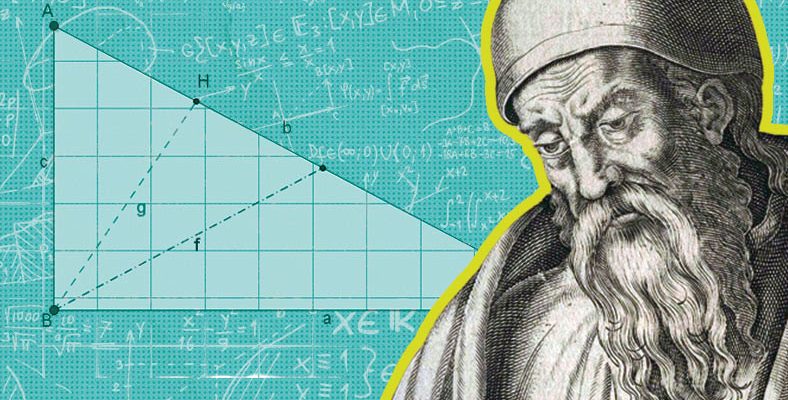
Make this article seo compatible,Let there be subheadings for the article, be in french, create at least 700 wordsLe mathématicien Euclide, dont les idées sont encore utilisées aujourd’hui même s’il a vécu il y a des milliers d’années, est considéré comme le fondateur de la géométrie. Euclide, qui a écrit de nombreux ouvrages qui n’ont pas survécu jusqu’à nos jours, en plus de son œuvre la plus célèbre, Elements, est connu pour le théorème d’Euclide qui porte son nom. Nous sommes sûrs que même lorsque nous parlons de mathématiques, beaucoup de gens ressentent de petites crampes au ventre car, avouons-le, en tant que pays, nous ne sommes pas très doués avec les chiffres. Mais ce qui est intéressant, a déterminé les règles de base des mathématiques il y a des milliers d’années La plupart des noms vivaient soit sur nos terres, soit dans des terres voisines. L’un de ces noms est Euclide, connu comme le fondateur de la géométrie. Lorsqu’on évoque Euclide, la première chose qui nous vient à l’esprit est le théorème d’Euclide, qui porte son nom. Ce théorème, qui a été expliqué avec différentes preuves par de nombreux mathématiciens à travers l’histoire, est décrit dans les Éléments, le seul livre écrit par Euclide qui nous soit parvenu. Le livre des Éléments est extrêmement important pour comprendre Euclide parce que le système d’axiomes qu’il a trouvé constitue la base de la géométrie. Expliquons brièvement pour ceux qui ne le savent pas : qui est Euclide ? On estime qu’Euclide est né à Alexandrie, en Égypte, en 330 avant JC et est mort au même endroit en 257 avant JC. C’est un ancien mathématicien. Nous disons estimé car on ne sait presque rien de la vie de ce personnage historique, également connu sous le nom d’Euclide d’Alexandrie. L’héritage le plus important qu’il nous a laissé est le livre de géométrie qu’il a appelé Elements. C’est pour cette raison qu’il est également considéré comme le fondateur de la géométrie. On dit qu’Euclide a en réalité écrit d’autres ouvrages que le livre des Éléments, mais aucun d’entre eux n’a survécu jusqu’à nos jours. Proclus, philosophe athénien qui vécut au Ve siècle après JC, Il dit qu’il a rassemblé le livre dispersé des Éléments. Stobaeus, qui a vécu à une époque similaire, dit qu’il a rassemblé les manuscrits les plus précis sur Euclide. Euclide a en fait rassemblé les éléments géométriques épars : En fait, les gens qui vivaient à l’époque d’Euclide et avant étaient en quelque sorte Ils traitaient de géométrie et de mathématiques et utilisaient des techniques appliquées. Par exemple, les habitants de l’Égypte ancienne calculaient des cercles et des carrés à l’aide de techniques appliquées. Ils ont pris le nombre pi comme étant 3,16, ce qui était très proche de la réalité. Les anciens Babyloniens possédaient d’importants travaux sur les mathématiques appliquées. Quand on regarde les tablettes qui ont survécu jusqu’à aujourd’hui, On voit qu’ils travaillent conformément au théorème de Pythagore. Euclide a pris tout cela, les a arrangés, les a vérifiés et a établi la géométrie en rassemblant ce qu’il a prouvé dans son livre Éléments. Dans le livre Elements, la géométrie est présentée comme un système d’axiomes : Le livre Elements préparé par Euclide est une sorte de manuel et Il se compose de 13 sous-rubriques divisées en 3 sections principales. Dans le livre où sont expliquées la géométrie plane, l’arithmétique, la théorie des nombres et la géométrie solide, il existe des idées communes appelées définitions, postulats et axiomes. Le livre présente tout cela comme une sorte de système d’axiomes. Certains postulats et axiomes expliqués dans le livre sont les suivants : Postulats ; Une ligne droite peut être tracée de n’importe quel autre point à n’importe quel point. Nous pouvons étendre un segment de droite de manière égale dans les deux directions. Un cercle peut être défini avec un centre ou un rayon. Tous les angles droits sont égaux les uns aux autres. Axiomes ; Les choses qui sont égales à quelque chose sont égales entre elles. Ajouter un montant égal à un montant égal rend le tout égal. Si nous soustrayons égal de égal, le reste sera égal. Les choses qui coïncident les unes avec les autres et ont les mêmes propriétés sont égales. Le tout est toujours plus grand que la partie. L’influence d’Euclide se poursuit encore aujourd’hui : À l’exception d’Elements, dont on sait qu’il a été écrit par Euclide. Données, Division des Formes Géométriques, Événements et Optique Il existe également d’autres études appelées. Ce ne sont pas des livres aussi complets que Elements, mais ce ne sont que quelques ouvrages, mais ils ont réussi à survivre jusqu’à aujourd’hui. Nous connaissons l’existence de ses livres, qui n’ont pas survécu jusqu’à nos jours, grâce aux références qui lui sont faites dans des manuscrits anciens. Presque jusqu’à la fin du XIXe siècle, le livre Éléments était considéré comme le raisonnement le plus précis et le plus parfait connu. Le livre Éthique, écrit par le philosophe hollandais Baruch de Spinoza au XVIIe siècle, Il a été calqué sur le livre Elements. Le livre Human Action, écrit par l’économiste autrichien Ludwig von Mises au XXe siècle, a également adopté la méthode d’Euclide. Alors, quel est le théorème d’Euclide ? Le théorème, aujourd’hui connu sous le nom de théorème d’Euclide, stipule qu’il existe une infinité de nombres premiers. Le théorème d’Euclide, qui fut ensuite prouvé par de nombreux mathématiciens, Il a été décrit par Euclide dans son livre Éléments. Pour résumer brièvement ; p1, p2, …, pn est une liste finie de nombres premiers. P = p1p2…pn. Si q = P + 1, alors q n’est pas premier ou premier. Les opérations varient selon qu’il s’agit d’un système principal ou non principal. Il existe également la relation euclidienne : D’après la figure ci-dessus ; h² = pxk b² = kxa c² = pxa Œuvres perdues qui auraient été écrites par Euclide : Mentionné dans les références des écrivains anciens Quelques œuvres écrites par Euclide Cependant, on pense qu’il n’a pas survécu jusqu’à nos jours. Par exemple, il a réalisé des études sur les sections coniques dans son livre intitulé Conics. Le même sujet a été expliqué plus en détail par Apollon de Perge. De nombreux travaux sur la mécanique sont attribués à Euclide, notamment dans les sources arabes. Ses études sur les surfaces appelées Planet Surface et ses travaux sur les erreurs de raisonnement appelés Le Livre des erreurs font partie des œuvres perdues d’Euclide. On pense qu’un autre livre intitulé Porism est un ouvrage sur la coupe conique, mais chacun a des idées différentes sur la signification du nom du livre. Considéré comme le fondateur de la géométrie Nous avons répondu à des questions fréquemment posées telles que qui est Euclide et quel est le théorème d’Euclide. Étant donné que les preuves basées sur les travaux d’Euclide contiennent des concepts numériques assez complexes, nous ne les avons pas inclus afin d’éviter toute confusion. $(function(){ //facebook window.fbAsyncInit = function() FB.init( appId : ‘1037724072951294’, xfbml : true, version : ‘v2.5’ ); ; (function(d, s, id) var js, fjs = d.getElementsByTagName(s)[0]; if (d.getElementById(id)) return; js = d.createElement(s); js.id = id; js.src = « https://connect.facebook.net/tr_TR/sdk.js »; fjs.parentNode.insertBefore(js, fjs); (document, ‘script’, ‘facebook-jssdk’)); $(‘body’).on( click: function() // facebook save button ajax FB.XFBML.parse(); , ‘.facebook-save’); // share scroll if ($(‘.content-sticky’).length > 0) { if ($(window).width() >= 768) { $(window).on(‘scroll’, function () { var scrollTop = $(this).scrollTop(); $(‘article’).each(function () if (scrollTop >= ($(this).find(‘.content-body’).offset().top – 76)) $(this).find(‘.content-sticky’).addClass(‘sticky’); if (scrollTop >= ($(this).find(‘.content-body’).offset().top + $(this).find(‘.content-body’).height() – ($(this).find(‘.content-sticky’).height() + 92))) $(this).find(‘.content-sticky’).removeClass(‘sticky’); $(this).find(‘.content-sticky’).css(‘bottom’: ‘0px’, ‘top’: ‘auto’); else $(this).find(‘.content-sticky’).addClass(‘sticky’).css( ‘bottom’: ‘initial’, ‘top’: ’76px’ ); else $(this).find(‘.content-sticky’).removeClass(‘sticky’).css(‘bottom’: ‘auto’, ‘top’: ‘0’); ); }); } } // share click $(‘body’).on({ click: function (){ var $this = $(this), dataShareType = $this.attr(‘data-share-type’), dataType = $this.attr(‘data-type’), dataId = $this.attr(‘data-id’), dataPostUrl = $this.attr(‘data-post-url’), dataTitle = $this.attr(‘data-title’), dataSef = $this.attr(‘data-sef’); switch(dataShareType) case ‘facebook’: FB.ui( method: ‘share’, href: dataSef, , function(response) if (response && !response.error_message) updateHit(); ); break; case ‘twitter’: shareWindow(‘https://twitter.com/intent/tweet?via=webtekno&text= »+encodeURIComponent(dataTitle) + » %E2%96%B6 ‘ + encodeURIComponent(dataSef)); updateHit(); break; case ‘gplus’: shareWindow(‘https://plus.google.com/share?url= » + encodeURIComponent(dataSef)); updateHit(); break; case « mail’: window.location.href= »https://www.webtekno.com/mailto:?subject= » + encodeURIComponent(dataTitle) +’&body=’+ encodeURIComponent(dataSef); //updateHit(); break; case ‘whatsapp’: window.location.href= »whatsapp://send?text= » + encodeURIComponent(dataTitle) +’ %E2%96%B6 ‘+ encodeURIComponent(dataSef); updateHit(); break; function shareWindow (url) window.open(url, « _blank », « toolbar=yes, scrollbars=yes, resizable=yes, top=500, left=500, width=400, height=400 »); function updateHit () { $.ajax({ type: « POST », url: dataPostUrl, data: contentId: dataId, contentType: dataType, shareType: dataShareType, success: function(data) { if ($(‘.video-showcase’).length > 0) {…
Source link -57
Customize this title in frenchLe premier nom qui vient à l’esprit lorsqu’on évoque la géométrie est Euclide. Nous avons expliqué le théorème d’Euclide dans sa forme la plus simple.